[3주차] 항해99 심화트랙 - 심화 자료구조 및 알고리즘 2

항해99

항해99 심화트랙 자료구조 & 알고리즘 3주 차가 거의 마무리되어간다. 이번 주에 공부했던 최소 신장 트리(MST, Minimum Spanning Tree), 이분 탐색(Binary Search)에 대해 정리 해보려고 한다.

 

---

 

✔️ 신장 트리(Spanning Tree), 최소 신장 트리 (Minimum Spanning Tree)

💡 신장 트리 (Spanning Tree)

신장 트리 예시 - 출처 : https://ssabi.tistory.com/60

사이클 예시 - 출처 : https://yonghwankim-dev.tistory.com/234

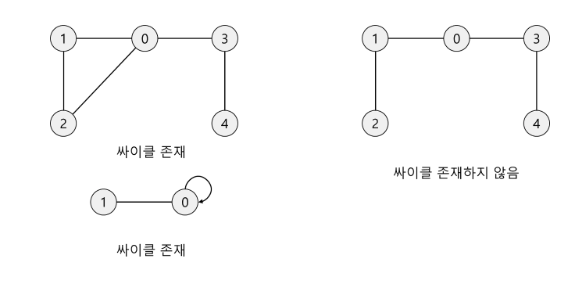
신장 트리(Spanning Tree)란 주어진 그래프의 모든 정점을 포함하면서 사이클을 형성하지 않는 부분 그래프이다. 여기서 사이클 이란, 한 노드에서 출발하여 간선(Edge)을 따라 다시 출발한 노드로 올 수 있는 상황을 일컫는다. 신장 트리는 모든 정점을 한 번씩 방문하면서, 정확히 하나의 경로를 통해 모든 정점을 연결한다.

 

'신장' 이란 용어가 '모든 정점을 포함' 또는 '모든 정점을 연결' 이라는 의미이다.

 

💡 최소 신장 트리 (Minimum Spanning Tree, MST)

예시 그래프

최소 신장 트리 -출처 : https://chanhuiseok.github.io/posts/algo-33

최소 신장 트리(MST)란 주어진 가중치가 있는 연결된 그래프에서 가장 작은 가중치합을 가지면서, 모든 노드를 포함하는 부분 그래프이다. 신장 트리와 마찬가지로, 트리의 성질에 따라 사이클을 포함하지 않는다.

 

최소 신장 트리는 다양한 분야에서 활용된다. 전기 회로, 도로 네트워크, 통신 네트워크 등 최소 비용으로 모든 지점을 연결하는 데 사용될 수 있다.

 

최소 신장 트리를 찾는 알고리즘은 크루스칼(Kruskal's algorithm) 알고리즘, 프림(Prim's algorithm) 알고리즘이 사용된다. 이 중에서 크루스칼 알고리즘에 대해 정리 해보도록 하겠다.

 

크루스칼 알고리즘 (Kruskal's algorithm)

크루스칼 알고리즘은 간선(Edge)의 가중치를 기준으로 그래프에서 최소 비용 부분 그래프인 신장 트리를 찾는 알고리즘이다. 가중치를 오름차순으로 정렬 후, 가중치가 제일 작은 간선을 선택한다. 단, 사이클이 형성되는 간선은 선택하지 않아야 한다.

 

1. 그래프의 간선을 가중치의 오름차순으로 정렬

간선 가중치 오름차순 정렬

2. 가중치가 가장 작은 간선 선택 (a-b)

가중치가 가장 작은 간선 선택

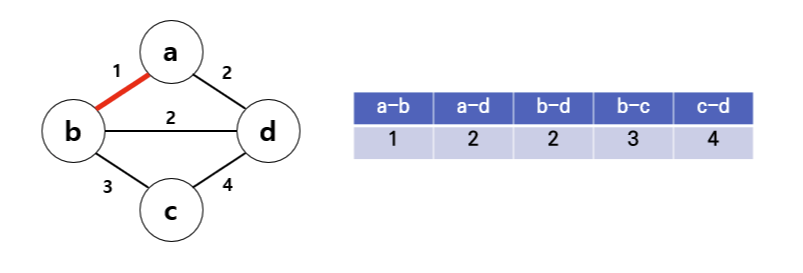
3. 다음으로 가중치가 작은 간선 선택 (a-d)

다음 작은 가중치 간선 선택

4. 다음으로 가중치가 작은 간선은 (b-d)이지만, 사이클 형성으로 인해 선택하지 않음

사이클 형성

5. 다음으로 가중치가 작은 간선 (b-c)를 선택하고, 선택한 간선의 개수가 정점-1 개가 되면 종료

최소 신장 트리 완료

사이클 여부 확인은?

이렇게 크루스칼 알고리즘으로 최소 신장 트리를 구해 나갈 때, 사이클을 확인하는 방법은 'union-find 알고리즘' 을 이용한다. 

 

Union-Find 알고리즘

서로소 집합(Disijoin-Set) 알고리즘 이라고도 하며, 원소들이 여러 그룹으로 나뉘어 있을 때 두 원소가 같은 그룹에 속해 있는지 여부를 효율적으로 판별하는 데 사용된다. 

 

이 알고리즘은 일반적으로 두 가지 연산을 지원한다.

 

• Union(합치기) : 두 원소가 속한 집합을 하나로 합친다.
• Find(찾기) : 특정 원소가 속한 집합의 대표(부모) 원소를 찾는다.

• parent 배열은 각 정점의 부모 정보를 저장하는 배열이다. 초기값으로 자기 자신을 설정한다.

 

• Union(1,2)를 진행한 모습이다.
• 정점 2의 부모가 1이 된다. (정점이 작은 것을 부모로 하도록 한다.)

• Union(1,4)를 진행한 모습이다.
• 정점 4의 부모가 1이 된다. (이 또한 정점이 작은 것을 부모로 하도록 한다.)

• Union(2,4)를 진행하려고 했더니, 이미 2와 4의 부모가 '1'로 같다.
• 이 경우는 사이클이 생기기 때문에 Union을 진행하지 않도록 한다.

 

---

 

📝 크루스칼 & Union-Find 활용 - 네트워크 연결 최소비용 구하기

[Baekjoon] 1922. 네트워크 연결 - https://www.acmicpc.net/problem/1922

1922번: 네트워크 연결

네트워크 연결 문제

N = int(input()) # 컴퓨터의 수
M = int(input()) # 연결할 수 있는 선의 수

# 부모 노드 찾기.
def find_parent(x):
    if x != parent[x]:
	    # 재귀적으로 최상위 부모를 찾는다
        parent[x] = find_parent(parent[x]) 
    return parent[x]

# 부모를 하나로 합쳐주기
def union_parent(a, b):
    a = find_parent(a)
    b = find_parent(b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

parent = [i for i in range(N + 1)] # 노드 번호 - 부모
edges = [] # 비용 & 간선

# 비용, 간선 정보 넣기
for _ in range(M):
    a, b, cost = map(int, input().split())
    edges.append((cost, a, b))
edges.sort() # 가장 적은 비용이 드는 간선 부터 선택하기 위해서 정렬

result_cost = 0
for cost, a, b in edges:
	# 이미 부모 노드가 같다면 사이클이 일어나기 때문에, 같다면 지나간다.
    if find_parent(a) != find_parent(b): 
        union_parent(a, b)
        result_cost += cost

print(result_cost)

모든 컴퓨터를 연결해야 하는 문제이다. 컴퓨터의 수와 컴퓨터를 연결할 때 드는 비용이 주어지면, 모든 컴퓨터의 네트워크를 연결할 때 드는 최소 비용을 구해야 한다. 위에서 정리한 크루스칼 알고리즘과 Union-Find 알고리즘을 활용하여 문제를 해결했다.

 

Union

# 부모를 하나로 합쳐주기
def union_parent(a, b):
    a = find_parent(a)
    b = find_parent(b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

정점 a와 b를 받아서 find_parend()로 부모를 찾는다. 정점 값이 더 작은 쪽이 부모가 되도록 Union 하여 parent 정보를 경신하는 역할을 하는 메서드이다.

 

Find

# 부모 노드 찾기.
def find_parent(x):
    if x != parent[x]:
        parent[x] = find_parent(parent[x]) # 재귀적으로 최상위 부모를 찾는다
    return parent[x]

정점 x를 한 개 받아서, 부모 정보를 가져오는 역할을 하는 메서드이다.

 

매개변수로 받은 x와 부모 리스트에 있는 parent[x]의 값이 같다면, 초기값에서 변경이 없었다는 의미(부모가 자기 자신)이다. 즉, Union 되지 않았다는 의미이다. 하지만 x != parent[x] 라면, 다른 정점과 Union 되었다는 의미(부모가 존재)이기 때문에 재귀적으로 최상위 부모를 찾아간다. 이후, 그 최상위 부모를 자신의 부모로 다시 갱신해주는 것이다.

 

결과적으로, Union-Find를 활용하여 효율적으로 부모를 찾고 사이클인지 아닌지 판별하여 네트워크 연결 최소 비용을 구할 수 있게 된다.

 

---

 

✔️ 이진 탐색 (Binary Search)

💡 이진 탐색 (Binary Search) 이란?

이진 탐색은 정렬된 배열에서 원하는 값을 효율적으로 찾는 알고리즘이다.

 

이 알고리즘은 배열의 중간 값과 찾고자 하는 값을 비교하여 배열을 반으로 나누고, 찾고자 하는 값이 왼쪽 혹은 오른쪽 부분 배열에 있을 경우, 해당 부분 배열에서 다시 중간 값을 찾아 찾고자 하는 값을 찾을 때까지 반복하는 알고리즘이다.

 

이진 탐색 과정

Binary Search 과정

1.  배열(리스트)의 중간 값과 찾고자 하는 값을 비교
2. 만약 중간 값이 찾고자 하는 값과 동일하다면 탐색 종료
3. 중간 값이 찾고자 하는 값보다 크다면, 중간 값의 왼쪽 배열 부분만 탐색
4. 중간 값이 찾고자 하는 값보다 작다면, 중간 값의 오른쪽 배열 부분 탐색
5. 탐색이 성공할 때까지 반복

 

이진 탐색 장점 & 단점

• 장점 : 이진 탐색은 중간 값을 기준으로 배열(리스트)을 반으로 나누어가며 탐색 범위를 절반으로 줄여나간다. 그렇기 때문에 모든 배열을 확인하는 순차 탐색(Sequantial Search) 보다 효율적이다. 순차 탐색 시간복잡도는 O(N)이지만, 이진 탐색의 시간복잡도는 O(logN)이다.
• 단점 : 이진 탐색을 사용하기 위해서는 정렬된 배열이 필요하다.

 

📝 이진 탐색 활용 - target 값 찾기

[Leetcode] 240. Search a 2D Matrix II

Search a 2D Matrix II - LeetCode

Leetcode 문제

문제 설명

N x M 2차원 리스트가 주어진다. 해당 리스트의 열, 행은 모두 오름차순 정렬이 되어있는 상태이다. 모든 행, 열을 탐색하여 target 값이 존재하면 True, 존재하지 않으면 False를 반환하는 문제이다.

 

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:

        for i in range(len(matrix)):
            # 행, 열 모두 오름차순 정렬이기 때문에, 
            # 첫 번째 값이 target보다 크면 앞으로 target은 나올 수 없다.
            if matrix[i][0] > target:
                return False

            left = 0
            right = len(matrix[i]) - 1
            while left <= right:
                mid = (left + right) // 2 # 중간값

                # 해당하는 target일 경우 바로 return
                if matrix[i][mid] == target:
                    return True

                # 중간 값이 target보다 작다면, mid를 옮겨주어 큰 값들이 있는 배열 탐색
                if matrix[i][mid] < target: 
                    left = mid + 1
                # 중간 값이 target보다 크다면, mid를 옮겨주어 작은 값들이 있는 배열 탐색
                else:
                    right = mid - 1

        return False

매트리스를 순회하면서 target 값이 존재하는지 확인해야 한다. 전체 탐색을 하게 되면 시간 복잡도는 O(N)이 된다.

 

하지만 우리는 이진 탐색을 공부했다.

 

매트리스의 조건으로 행, 열이 모두 정렬되어 있으니 이진 탐색을 적용할 수 있다. 시간 복잡도를 O(logN)으로 줄일 수 있게 된다.

 

---

✍️ 글을 마치며

벌써 항해99 정규 트랙이 시작된지 3주가 넘었다.

 

나는 전공자지만, 지금 생각해보면 알고리즘과 자료구조에 대한 공부가 매우 부족했었던 것 같다.

 

1주차에 처음 알고리즘을 풀 때, 시간 복잡도와 공간 복잡도에 대해서 크게 신경쓰지 않았었다. 가장 큰 나의 문제였다.

 

그래서 나는 알고리즘 주차를 거듭하며 문제를 풀때, 나의 답에 대한 시간 복잡도를 계속 생각하고, 어떤 알고리즘을 적용하면 시간 복잡도를 줄일 수 있을지 계속 고민하며 해결하려고 노력했다.

 

1주차에 비해서 자료구조, 알고리즘에 대한 시간 복잡도에 대한 이해도와 문제 해결력이 꽤 나아진 것 같은 기분이다.

 

하지만 현재도 많이 부족하다. 앞으로 많은 문제를 풀어가며, 지금처럼 꼭 시간 복잡도에 대해 생각하고 공간 복잡도에 대해 생각하며 푸는 습관을 유지하고싶다.

 

요즘 시간이 너무 빨리 가는 것 같다. 눈 깜짝하면 아침에서 밤이 되어있는데, 열심히 하고 있다는 증거로 생각하며 앞으로 더 힘내서 수료할 때 까지 나아가고싶다.

 

후회없이 열심히 공부한 3개월로 기억될 수 있도록 열심히 해보자.